QUICK REVIEW

PHYSICS

Physics is the branch of science that studies the nature and behavior of matter, energy, and the interaction between them

 The main Branches of Physics
Physics is constituted of many interdisciplinary subjects and branches for those interested in
making a career in this field. Here are all branches of Physics:
1. Classical Physics
2. Modern Physics
3. Nuclear Physics
4. Atomic Physics
5. Geophysics
6. Biophysics
7. Mechanics
8. Acoustics
9. Optics
10. Thermodynamics
11. Astrophysics

INTERNATIONAL SYSTEM OF UNITS (SI)

.

Basic quantity	Symbol of Basic Quantity	Name of the Base SI units	Symbol of SI units
Time	T	Second	s
Length	L	Metre	m
Mass	M	Kilogram	kg
Temperature	T, θ	Kelvin	K
Electric current	I	Ampere	A
Amount of substance	n	Mole	mol
Luminous intensity	lv	Candela	cd

PREFIXES FOR SI UNITS

Value	Prefix	Symbol
1024	yotta	Y
1021	Zetta	Z
1018	exa-	E
1015	peta-	P
1012	tera-	T
109	giga-	G
106	mega-	M
103	kilo-	K
102	hecto-	h
101	deca-	da
10-1	deci-	d
10-2	centi-	c
10-3	milli-	m
10-6	Micro	μ
10-9	nano-	n
10-12	pico-	p
10-15	femto-	f
10-18	atto-	a
10-21	zepto	z
10-24	yocto	y

 

SUPPLEMENTARY UNIT:

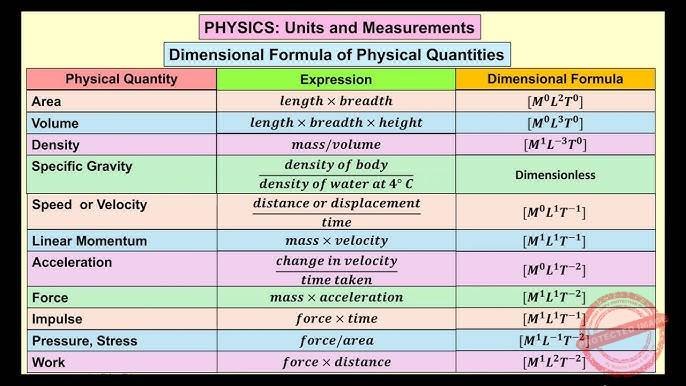
DIMENSION

The dimension of a physical quantity is the power of the fundamental quantities in terms of which it can be represented. Each of the basic quantities is called “ dimension”  Or

The word dimension has a special meaning in physics. It is used to denote the nature of the physical quantity. 

DIMENSION	Symbol
Time	[T]
Length	[L]
Mass	[M]
Temperature	[T], [θ]
Electric current	[A]

SIGNIFICANT FIGURES

The number of accurately known digit and first doubtful digit( called least significant)

are known as significant figures or significant digit.

RULES OF DETERMINATION SIGNIFICANT FIGURES

ALL non-zero numbers (1,2,3,4,5,6,7,8,9) are ALWAYS significant

EXAMPLE

• 3423                                       (ii)     457435                                   

4- significant figure                           6 -significant figure                  

(iii)    587                                          (iv) 58

3- significant figure                         2- significant figure

ALL zeroes between non-zero numbers are ALWAYS significant

EXAMPLE

• 3003                                       (ii)     009                                              

4- significant figure                           5 -significant figure

          (iii)    507                                          (iv)   5000097                

3- significant figure                             3- significant figure

 

Zeros locating the position of decimal in numbers of magnitude less than one are not significant

EXAMPLE

• 0063                                    (ii)     0.009                                      

2- significant figure                            1 -significant figure

          (iii)    0.0000307                                (iv) 0.0009078

3- significant figure                            4 -significant figure

Final zeros to the right of the decimal point are significant.

EXAMPLE

• 0500                                    (ii)     0.00900                         

5- significant figure                            3 -significant figure

(iii)    9.00300                                   (iv) 0.090200

6- significant figure                            5- significant figure

 

Zeros at the end of the numbers greater than one may are may not be significant

EXAMPLE

• 700                                         (ii)     980000                                   

1- significant figure                            2- significant figure

 For any value written in scientific notation as A × 10^x, the number of significant figures is determined by applying the above rules only to the value of A.

EXAMPLE

4.5 × 10³ has two significant figures

4.50 × 10^-9 has three significant figures

4.500 × 10²³ has four significant figures

COMBINING UNCERTAINTY: ADDING AND SUBTRACTING

Q-1    The length of a copper wire at 30°C is 18.2 ± 0.04 cm and at 60°C is 19.7 ± 0.02 cm. Find the absolute uncertainty and die extension of the wire.

DATA

The length  L₁  = 18.2 ± 0.04

The length  L₂  = 19.7 ± 0.02

 SOLUTIONS

 Extension of the wire

L =  (L₂    –  L₁ )

L = (19.7-18.2) 

L  =  1.5mm

Absolute uncertainty

∆L =  ∆L₁  +  ∆L₂

 ∆L = 0.04 +0.02

∆L = 0.06

Extension of the wire with uncertainty = (  L  ±  ∆L )

Extension of the wire with uncertainty = ( 1.5   ±  0.06 ) mm

Q-   w = (4.52 ± 0.02) cm, x = ( 2.0 ± 0.2) cm, y = (3.0 ± 0.6) cm. Find z = x + y – w and

its uncertainty.

DATA w = (4.52 ± 0.02) cm x = ( 2.0 ± 0.2) cm y = (3.0 ± 0.6) cm SOLUTIONS Dz = Dx + Dy + Dw Dz  = 0.2 + 0.6 + 0.02 Dz = 0.82

So        z = x +y -w              z = 2.0  +3.0  -4.52                 z = 5.0  -4.52                 z = 0.48 cm Answer with uncertainty            Z  =  (z   ± ∆z ) cm            Z  =  (0.48 ± 0.82) cm

Q-    Three objects have masses of 3 ± 0.1 kg, 7 ± 0.1 kg, and 4 ± 0.05 kg. What is the uncertainty in the total mass of the three objects? 

DATA m1 = (3 ± 0.1 ) kg m2 = (7 ± 0.1 ) kg m3  =  (4 ± 0.05) kg  SOLUTIONS. m  = m1 + m1 + m1 = m =   3 +  7  +  4  = 14 kg

∆m = ∆ m1  +   ∆ m2 +  ∆ m3 ∆m =  0.1 + 0.1 + 0.05 ∆m =  0.25 Answer with uncertainty   =   m  ±  ∆m   =   (14  ±  0.25 ) kg