New
Popular

Chapter 11: Oscillation

Oscillation refers to the repeated back-and-forth movement of something between two positions or states. An oscillation can be a periodic motion that repeats itself in a regular cycle. The large amplitude oscillations in a system produced by a small amplitude driving force , which has a frequency equal to the natural frequency is called resonance

Untitled design (1)-modified

Imran Hashmi

Associate professor

Chapter Content:

Chapter notes:
UNIT-11 -oscillation-no
Chapter numerical
chapter-11- Oscillation-num
Chapter multiple choice questions:
Chapter-11-MCQs-oscillations

ASSIGMENT UNIT-11 OSCILLATIONS.

PERIOD ,  FREQUENCY,   DISPLACEMENT AND VELOCITY

1          The processor of a certain computer operates at 3.70 GHz, How much time is required for one processing                      cycle?   [  2.7  x 10 -10 s  ]

2          Two baseball players warm up with a game of catch. If it takes 6.6 s for the ball to go from one player to the                    other and then back to the first, what is the frequency of the ball’s motion?           [   0.15 Hz ]

3          When dragonflies hover, they tend to “bob” up and down with a motion that is an excellent approximation to                    simple harmonic motion. Suppose that a dragonfly is at x = A at time t = 0, and that its bobbing motion has an                amplitude of A = 0.40 cm and a period of T = 0.24 s. Find (a) the position at the time t = 0.10 s   

 [ first find ω t , Then, using the formula  x = A cos ωt   ]     Ans  [   -0.34 cm ]                                            Picture1

4          A piece of paper completes 50 vibrations in 5 s  when some waves pass through the surface of water. Find the               time period and the frequency of the piece of paper. If the wavelength of the wave is 10cm, find the velocity of                 the waves         [T = 0.1s ,    10 Hz,   1.0 m ]

5          A body vibrates with a time period of 1/256 s,   producing waves which travel with a velocity of 350 cm/s.                          Calculate the wavelength of emitted wave.                [ λ = 896 m] 

SPRING - MASS SYSTEM

1          When a family of four with a total mass of 200 kg steps into their 1200-kg car, the car’s springs compress 3.0                  cm.  What is the spring constant of the car’s springs [   6.5 X 104  N /m ]

2          A horizontal spring with a force constant of 11 N/ m is connected to an air-track cart. When the cart is set in                    motion, the spring causes it to oscillate back and forth with a period of 1.2 s. What is the mass of the cart?

            [ 0.4 Kg ]

3          When  m1 = 0.420-kg mass air-track cart is attached to a horizontal spring, it oscillates with a period of 0.350 s.              If, instead, a different cart with mass m2 is attached to the same spring, it oscillates with a period of 0.700 s.                    Find (a) the force constant of the spring and (b) the mass m2. [ 135 N/m,    1.86 kg  ]

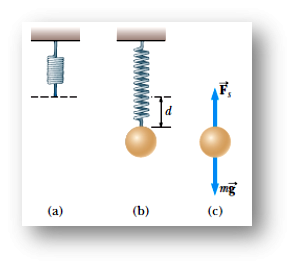
4          A common technique used to measure a spring constant is illustrated in Figure 13.2. A spring is hung vertically                 (Fig. a), and an object of mass m is attached to the lower end of the spring and slowly lowered a distance d to               the equilibrium point (Fig. b). Find the value of the spring   constant if the spring is displaced by 2.00 cm and                 the mass is 0.550 kg.  [ 2.7 x 102 N/m     Hint  Fg + Fs = 0  ⇒  -mg + kd = 0  ⇒ k  = mg/d ]

Picture1

5.      The period of vibration of a body of mass 25 g attached to a spring., Vibrates on a smooth horizontal surface.                 When it is displaced 10 cm ot the right of its extreme position, the period of vibration is 1.57 seconds and the                   velocity at the end of this displacement is 0.4 m/s. determine the (a) spring constant, (b) total energy                               (c)  amplitude of the vibration. [ 0.4 N/m,      4 x 10-3 J.  ,         0.1414 m  ]

6.         A body hanging from a spring is set into motion and the period of oscillation is to be 0.8 s. After the body has                 come to rest, it is removed. How much shorter will the spring be when it comes to rest? [ x = 6.2 cm ] 

7.         A mass at the end of a spring oscillates with simple harmonic motion with a period of 0.40 s; find the                               acceleration when the displacement is 4.0 cm.   [  a = -9.87 m/s2 ]

8.      A body of mass 32 g attached to an elastic spring is performing SHM. Its velocity is 0.4 m/s when the                               displacement is 8 cm to the right. If the spring constant is 0.4 N/m. Calculate (i) total energy (ii) the amplitude of             its motion [ 3.84 x 10-3 J,     x0 = 0.1385 m  ]

SIMPLE PENDULUM

1          Calculate the length of the Second’s pendulum at a  place where g = 9.8 m/s2   [  0.99 m  ]

2         Compute the acceleration due to gravity on the surface of the moon where a simple pendulum 1.5 m long                       makes 100 vibrations in 605 seconds [ gm = 1.617 m/s2 ]

3         Find the length of the second’s pendulum on the planet Jupiter, where the value of ‘g’ is 2.63 times that of the               ‘g’ on the surface of Earth. [ L  = 0.226 m ]

4         A simple pendulum completes 4 vibrations in 8 seconds on the surface of the Earth. Find the period on the                     surface of the moon where the acceleration due to gravity is one-sixth that of Earth. [ 4.9 seconds ]

5         Calculate the length of a simple pendulum whose frequency of vibration f = 0.5 vib/sec.     [0.993m]

6         The pendulum on a cuckoo clock is 5.0 cm long. What is its frequency? [ g = 9.8 m/s2    Ans  f = 2.28 Hz ]

Download Assignment